摘自:https://www.cnblogs.com/chengxiao/p/6059914.html
摘自:https://www.cnblogs.com/dijia478/p/8006713.html
数据结构
HashMap中的数据结构是数组+单链表的组合,以键值对(key-value)的形式存储元素的,通过put()和get()方法储存和获取对象。
什么是哈希表(hash table)
在讨论哈希表之前,我们先大概了解下其他数据结构在新增,查找等基础操作执行性能
数组:采用一段连续的存储单元来存储数据。对于指定下标的查找,时间复杂度为O(1);通过给定值进行查找,需要遍历数组,逐一比对给定关键字和数组元素,时间复杂度为O(n),当然,对于有序数组,则可采用二分查找,插值查找,斐波那契查找等方式,可将查找复杂度提高为O(logn);对于一般的插入删除操作,涉及到数组元素的移动,其平均复杂度也为O(n)
线性链表:对于链表的新增,删除等操作(在找到指定操作位置后),仅需处理结点间的引用即可,时间复杂度为O(1),而查找操作需要遍历链表逐一进行比对,复杂度为O(n)
二叉树:对一棵相对平衡的有序二叉树,对其进行插入,查找,删除等操作,平均复杂度均为O(logn)。
哈希表:相比上述几种数据结构,在哈希表中进行添加,删除,查找等操作,性能十分之高,不考虑哈希冲突的情况下,仅需一次定位即可完成,时间复杂度为O(1),接下来我们就来看看哈希表是如何实现达到惊艳的常数阶O(1)的。
我们知道,数据结构的物理存储结构只有两种:顺序存储结构和链式存储结构(像栈,队列,树,图等是从逻辑结构去抽象的,映射到内存中,也这两种物理组织形式),而在上面我们提到过,在数组中根据下标查找某个元素,一次定位就可以达到,哈希表利用了这种特性,哈希表的主干就是数组。
比如我们要新增或查找某个元素,我们通过把当前元素的关键字 通过某个函数映射到数组中的某个位置,通过数组下标一次定位就可完成操作。
存储位置 = f(关键字)
其中,这个函数f一般称为哈希函数,这个函数的设计好坏会直接影响到哈希表的优劣。举个例子,比如我们要在哈希表中执行插入操作:
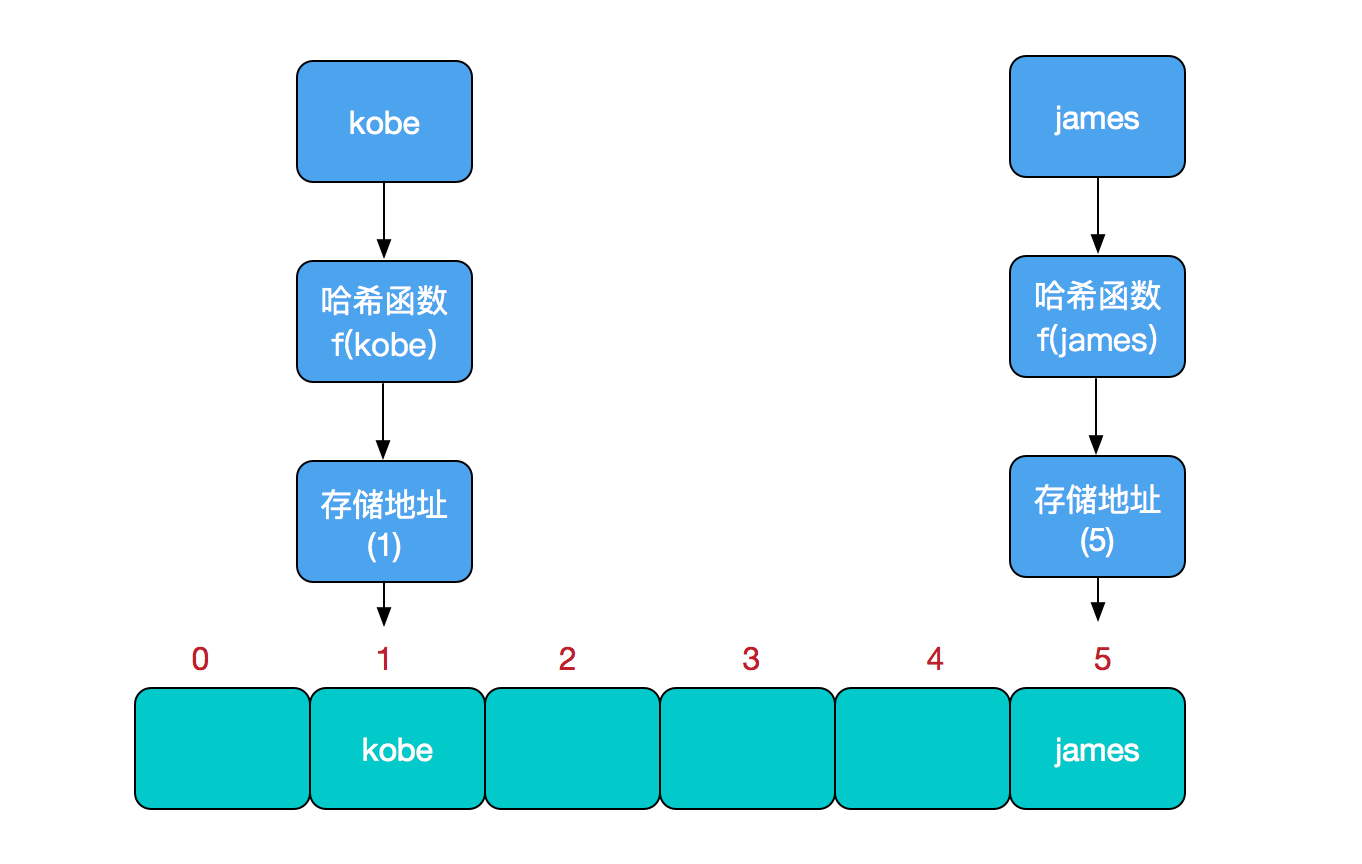
查找操作同理,先通过哈希函数计算出实际存储地址,然后从数组中对应地址取出即可。
哈希冲突
然而万事无完美,如果两个不同的元素,通过哈希函数得出的实际存储地址相同怎么办?也就是说,当我们对某个元素进行哈希运算,得到一个存储地址,然后要进行插入的时候,发现已经被其他元素占用了,其实这就是所谓的哈希冲突,也叫哈希碰撞。前面我们提到过,哈希函数的设计至关重要,好的哈希函数会尽可能地保证计算简单和散列地址分布均匀,但是,我们需要清楚的是,数组是一块连续的固定长度的内存空间,再好的哈希函数也不能保证得到的存储地址绝对不发生冲突。那么哈希冲突如何解决呢?哈希冲突的解决方案有多种:开放定址法(发生冲突,继续寻找下一块未被占用的存储地址),再散列函数法,链地址法,而HashMap即是采用了链地址法,也就是数组+链表的方式。
HashMap实现原理
整体结构
HashMap的主干是一个Entry数组。Entry是HashMap的基本组成单元,每一个Entry包含一个key-value键值对。
1 | /** |
Entry是HashMap中的一个静态内部类:
1 | static class Entry<K,V> implements Map.Entry<K,V> { |
HashMap的整体结构如下:
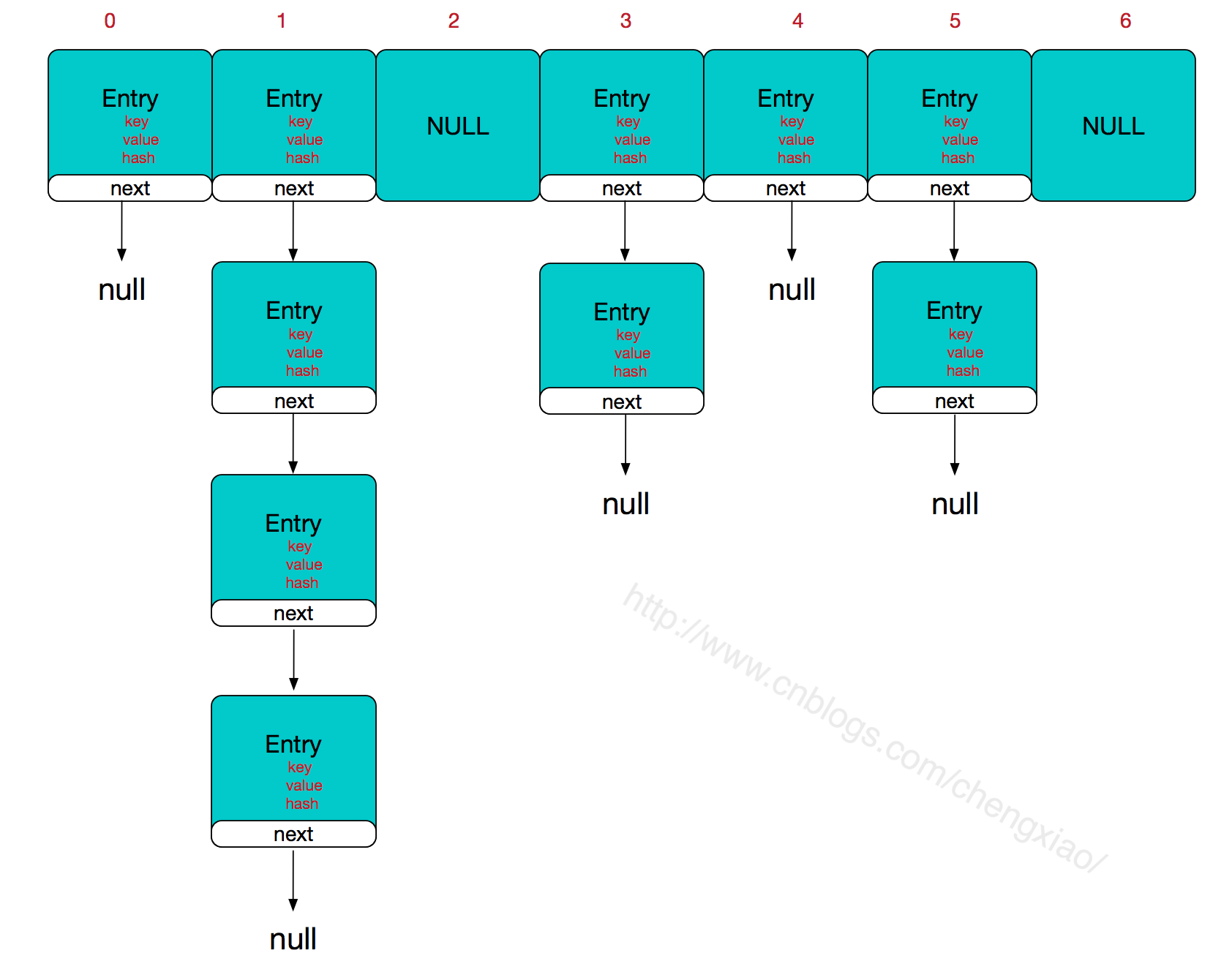
简单来说,HashMap由数组+链表组成的,数组是HashMap的主体,链表则是主要为了解决哈希冲突而存在的,如果定位到的数组位置不含链表(当前entry的next指向null),那么对于查找,添加等操作很快,仅需一次寻址即可;如果定位到的数组包含链表,对于添加操作,其时间复杂度为O(n),首先遍历链表,存在即覆盖,否则新增;对于查找操作来讲,仍需遍历链表,然后通过key对象的equals方法逐一比对查找。所以,性能考虑,HashMap中的链表出现越少,性能才会越好。
其他几个重要字段
1 | //初始容量 16 而且容量必须为2的n次幂 |
构造器
1 |
|
注:
此处仅用于接收初始容量大小(
capacity)、加载因子(Load factor),但仍无真正初始化哈希表,即初始化存储数组table此处先给出结论:**真正初始化哈希表(初始化存储数组
table)是在第1次添加键值对时,即第1次调用put()时。
PUT方法
1 | public V put(K key, V value) { |
初始化哈希表
inflateTable这个方法用于为主干数组table在内存中分配存储空间,通过roundUpToPowerOf2(toSize)可以确保capacity为大于或等于toSize的最接近toSize的二次幂,比如toSize=13,capacity=16;to_size=16,capacity=16;to_size=17,capacity=32.
1 | private void inflateTable(int toSize) { |
1 | private static int roundUpToPowerOf2(int number) { |
roundUpToPowerOf2中的这段处理使得数组长度一定为2的次幂,Integer.highestOneBit是用来获取最左边的bit(其他bit位为0)所代表的数值.
hash函数
1 | final int hash(Object k) { |
以上hash函数计算出的值,通过indexFor进一步处理来获取实际的存储位置
1 | static int indexFor(int h, int length) { |
h&(length-1)保证获取的index一定在数组范围内,举个例子,默认容量16,length-1=15,h=18,转换成二进制计算为
1 | 1 0 0 1 0 |
最终计算出的index=2。有些版本的对于此处的计算会使用 取模运算,也能保证index一定在数组范围内,不过位运算对计算机来说,性能更高一些(HashMap中有大量位运算),所以最终存储位置的确定流程是这样的:

再来看看addEntry的实现:
1 | void addEntry(int hash, K key, V value, int bucketIndex) { |
通过以上代码能够得知,当发生哈希冲突并且size大于阈值的时候,需要进行数组扩容,扩容时,需要新建一个长度为之前数组2倍的新的数组,然后将当前的Entry数组中的元素全部传输过去,扩容后的新数组长度为之前的2倍,所以扩容相对来说是个耗资源的操作。
插入更新示意图

为何HashMap的数组长度一定是2的次幂?
1 | void resize(int newCapacity) { |
如果数组进行扩容,数组长度发生变化,而存储位置 index = h&(length-1),index也可能会发生变化,需要重新计算index,我们先来看看transfer这个方法
1 | void transfer(Entry[] newTable, boolean rehash) { |
这个方法将老数组中的数据逐个链表地遍历,扔到新的扩容后的数组中,我们的数组索引位置的计算是通过 对key值的hashcode进行hash扰乱运算后,再通过和 length-1进行位运算得到最终数组索引位置。
hashMap的数组长度一定保持2的次幂,比如16的二进制表示为 10000,那么length-1就是15,二进制为01111,同理扩容后的数组长度为32,二进制表示为100000,length-1为31,二进制表示为011111。从下图可以我们也能看到这样会保证低位全为1,而扩容后只有一位差异,也就是多出了最左位的1,这样在通过 h&(length-1)的时候,只要h对应的最左边的那一个差异位为0,就能保证得到的新的数组索引和老数组索引一致(大大减少了之前已经散列良好的老数组的数据位置重新调换),个人理解。
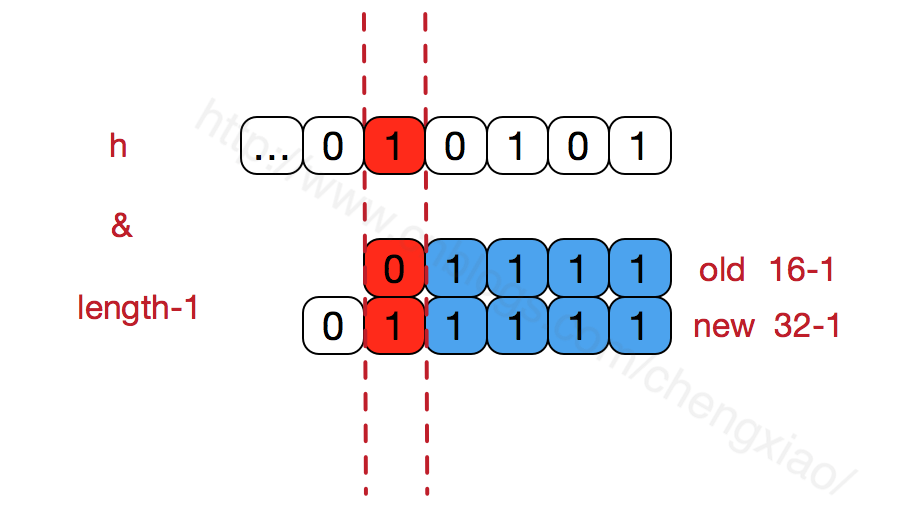
还有,数组长度保持2的次幂,length-1的低位都为1,会使得获得的数组索引index更加均匀,比如:
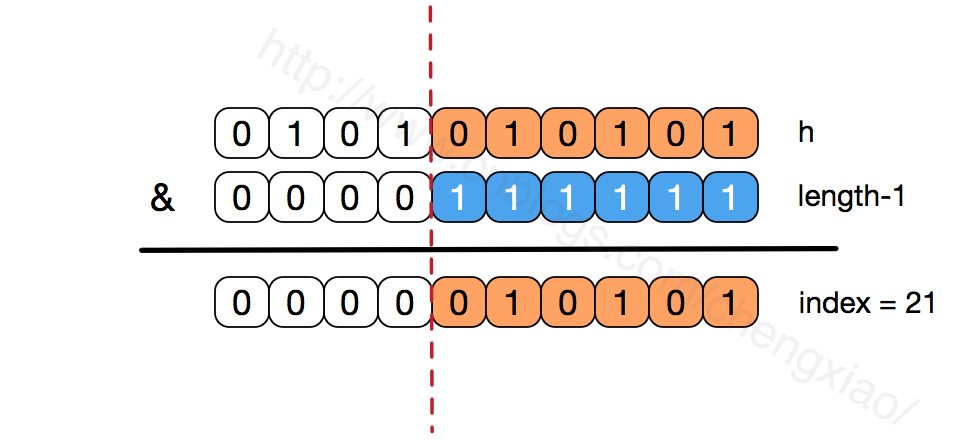
我们看到,上面的&运算,高位是不会对结果产生影响的(hash函数采用各种位运算可能也是为了使得低位更加散列),我们只关注低位bit,如果低位全部为1,那么对于h低位部分来说,任何一位的变化都会对结果产生影响,也就是说,要得到index=21这个存储位置,h的低位只有这一种组合。这也是数组长度设计为必须为2的次幂的原因。
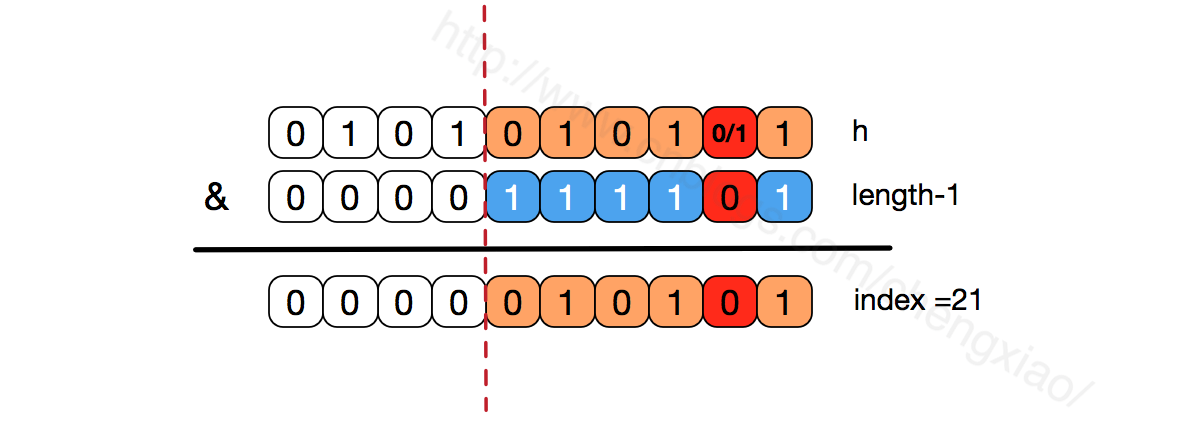
如果不是2的次幂,也就是低位不是全为1此时,要使得index=21,h的低位部分不再具有唯一性了,哈希冲突的几率会变的更大,同时,index对应的这个bit位无论如何不会等于1了,而对应的那些数组位置也就被白白浪费了。
GET方法
1 | public V get(Object key) { |
get方法通过key值返回对应value,如果key为null,直接去table[0]处检索。我们再看一下getEntry这个方法
1 | final Entry<K,V> getEntry(Object key) { |
可以看出,get方法的实现相对简单,key(hashcode)–>hash–>indexFor–>最终索引位置,找到对应位置table[i],再查看是否有链表,遍历链表,通过key的equals方法比对查找对应的记录。
总结
数据结构 & 主要参数

添加 & 查询数据流程
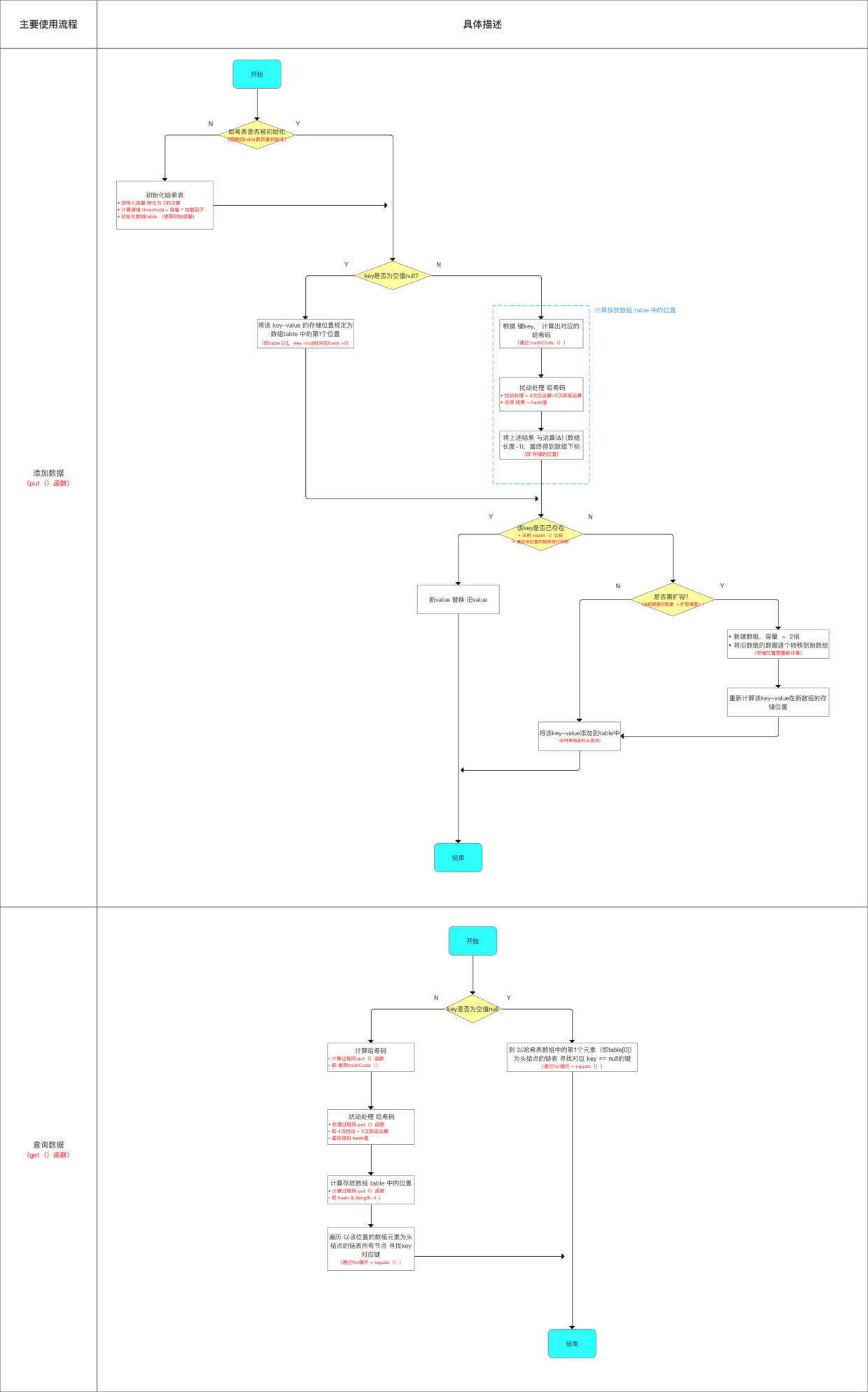
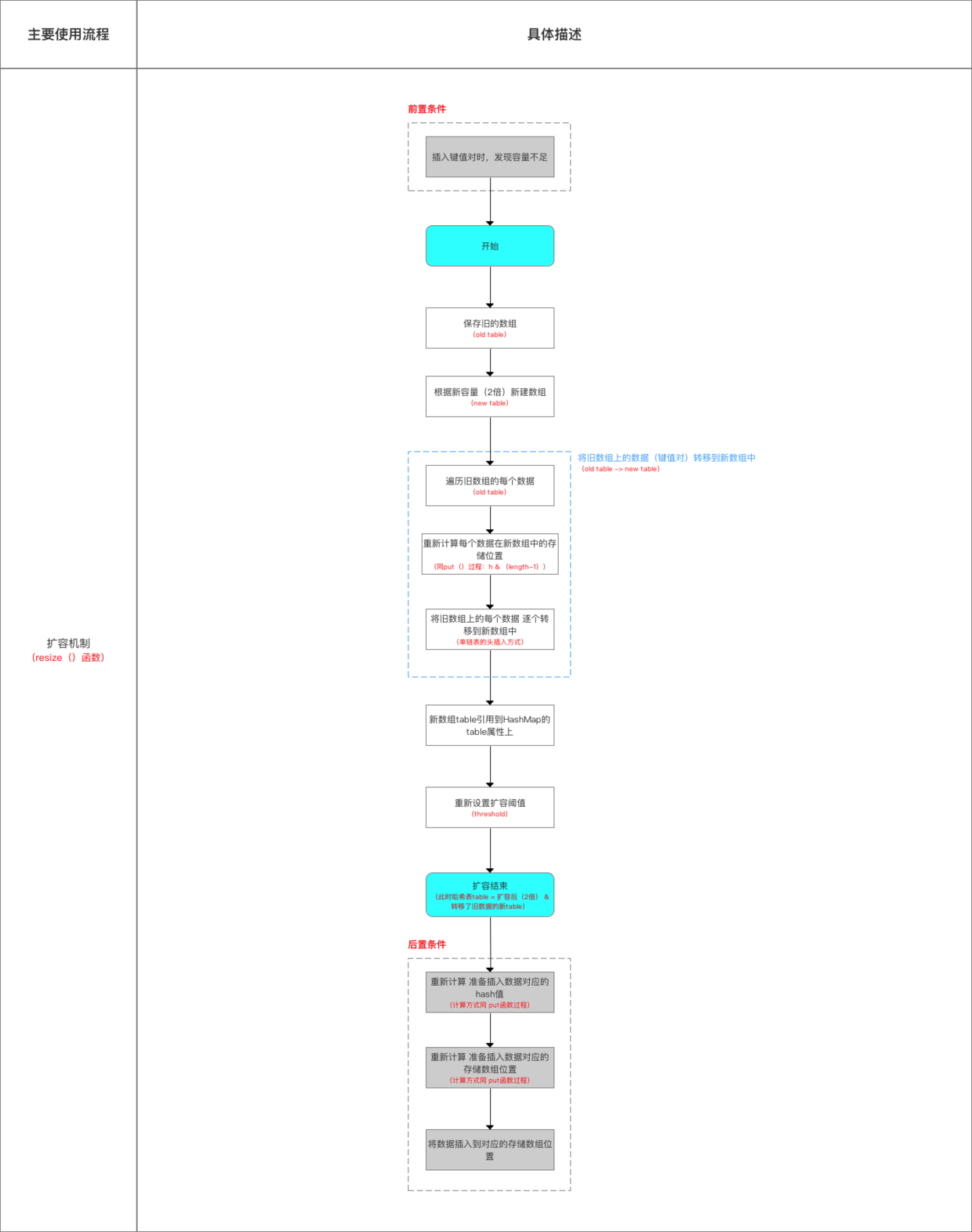
扩容机制